Le corrolaire du théorème des valeurs intermédiaires (théorème de la bijection)

Quand doit-on l’utiliser ?

Lorsque la question ressemble à

Quels sont les conditions pour l’appliquer ?

Ce sont les mêmes conditions que pour le théorème des valeurs intermédiaires, auxquelles on ajoute :

• la fonction $f$ doit être strictement monotone (croissante ou décroissante) sur l’intervalle $\left[a;b\right]$

Exemple

Solution rédigée

On admettra que la fonction $f$ est strictement croissante sur $\left[-3;+\infty\right[$. En général, l’étude du sens de variations est fait dans une question précédente.

• La fonction $f$ est continue sur l’intervalle $\left[-3;+\infty\right[$, car c’est la composée de deux fonctions continues.
• De plus, elle est strictement croissante sur $\left[-3;+\infty\right[$.
• $f(-3)=$$\textcolor{#FF0000}{1}$ et $\lim\limits_{\substack{x \rightarrow +\infty }} f(x)=$$\textcolor{#0000FF}{+\infty}$ donc $1 \in \left[\textcolor{#FF0000}{1}; \textcolor{#0000FF}{+\infty}\right[$.

Donc, d’après le théorème de la bijection, l’équation $f(x)=1$ admet une unique solution dans l’intervalle $\left[-3;+\infty\right[$.

Interprétation graphique

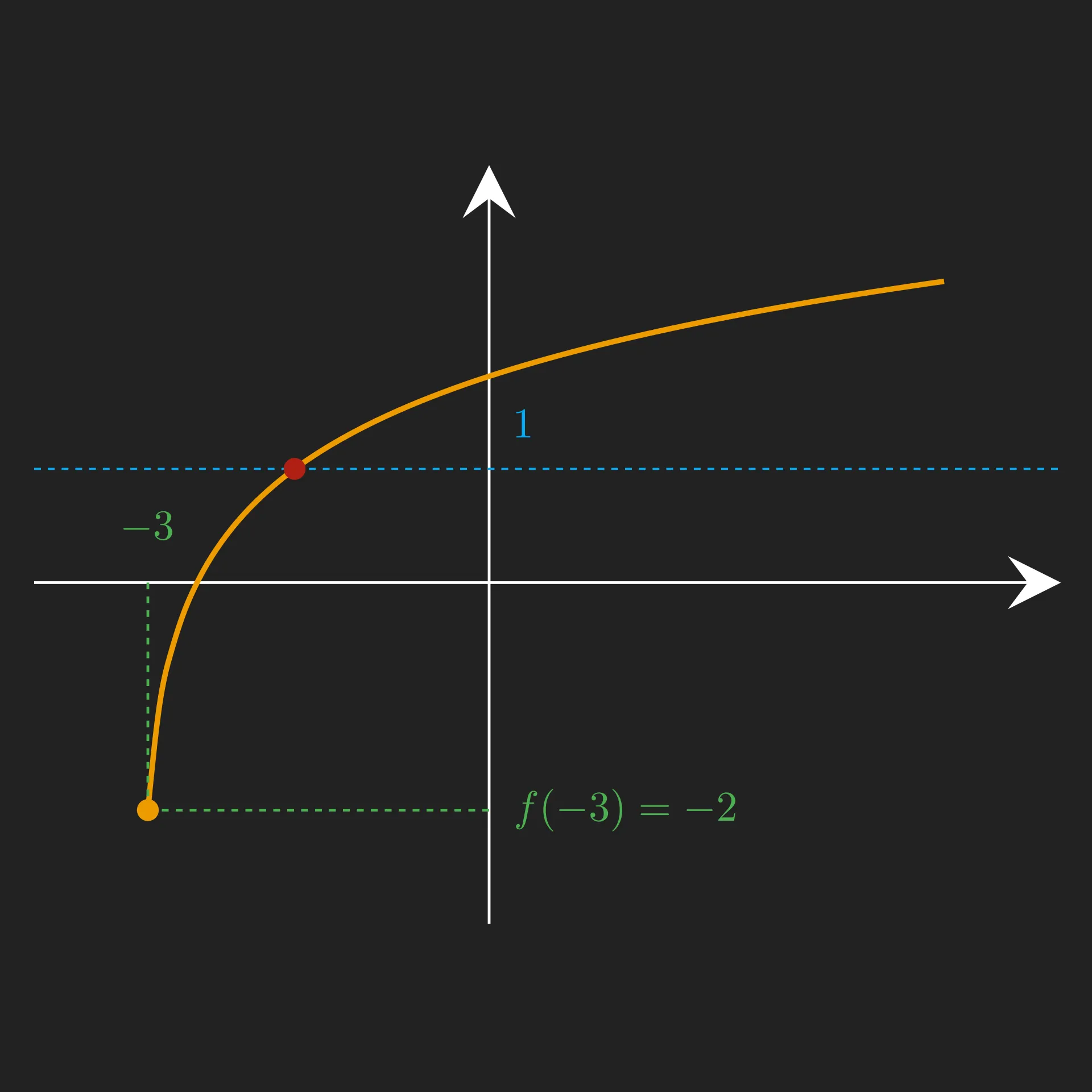
Exercices