Le théorème des valeurs intermédiaires
Quand doit-on l’utiliser ?
Lorsque la question ressemble à
Montrer que l’équation f(x)=k a au moins une solution dans l’intervalle [a;b]
Quels sont les conditions pour l’appliquer ?
Il faut que :
- la fonction f soit continue sur l’intervalle [a;b]
- le nombre k soit dans l’intervalle [f(a);f(b)] ou [f(b);f(a)] (selon lequel est le plus grand).
Remarque : f(a) ou f(b) peuvent être remplacés par x→alimf(x) ou x→blimf(x) lorsque la fonction est définie par exemple sur ]a;+∞[.
Exemple
Soit f la fonction définie sur [−3;+∞[ par f(x)=x3+3x2−x−2.
Montrer que l’équation f(x)=3 admet au moins une solution dans l’intervalle [−3;+∞[.
Solution rédigée
- la fonction f est continue sur l’intervalle [−3;+∞[, car c’est une fonction formée par le quotient de deux polynômes (qui sont toujours continus sur R).
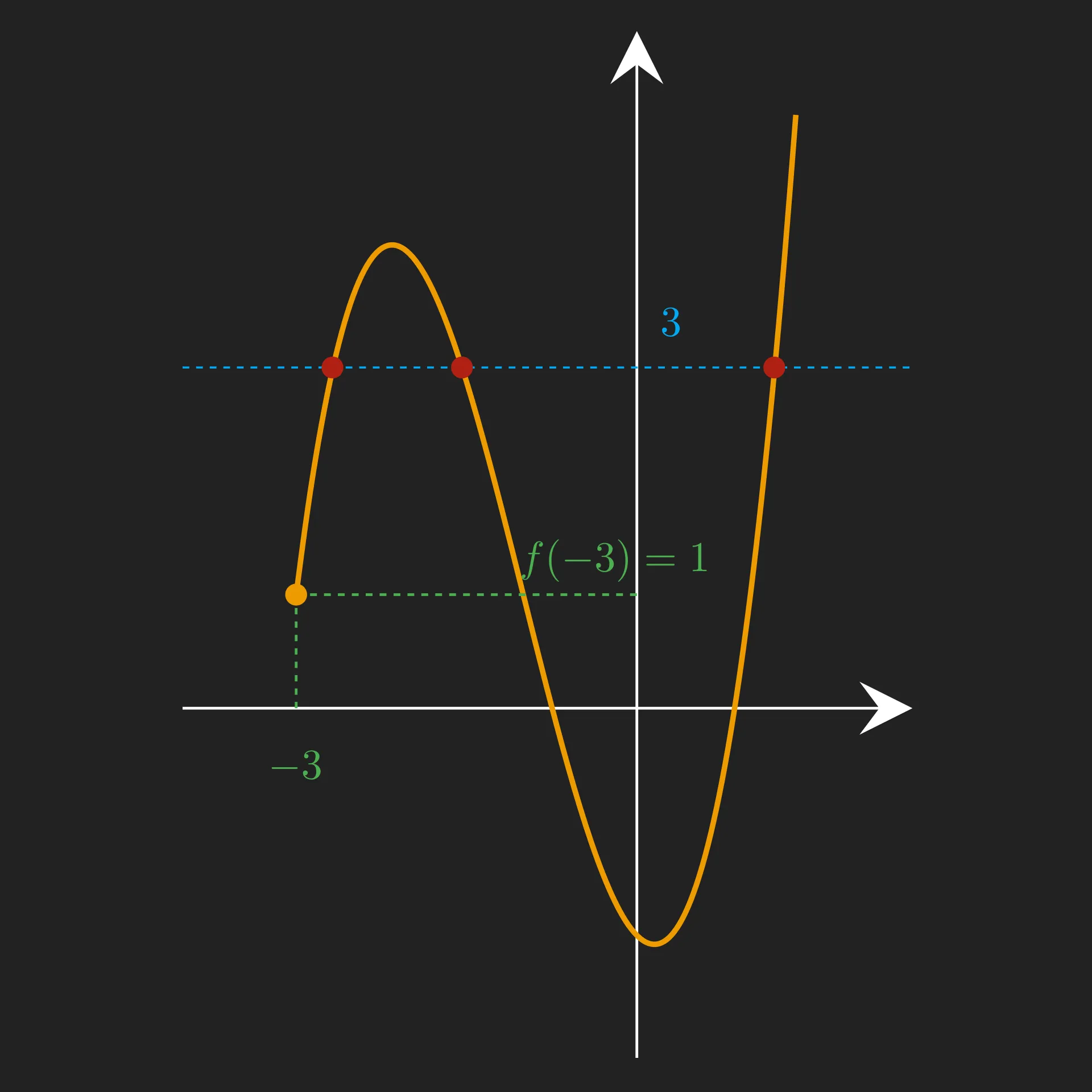
- f(−3)=1 et x→+∞limf(x)=+∞ donc 3∈[1;+∞[.
Donc, d’après le théorème des valeurs intermédiaires, l’équation f(x)=3 admet au moins une solution dans l’intervalle [−3;+∞[.
Interprétation graphique